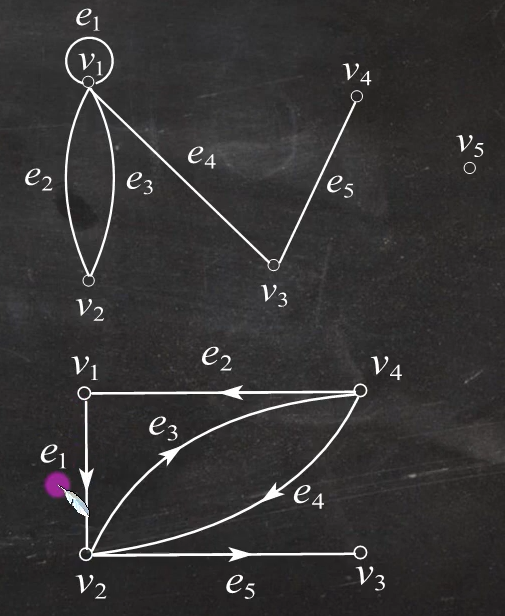离散数学速成
命题
命题:能判断真值的陈述句
真值:真和假(可以用1和0表示)
真命题:真值为真的命题
假命题:真值为假的命题
原子命题:不能再被分解的每题
复合命题:由原子命题通过联结词联结而成的命题
如何判断:
①是否为陈述句
②是否有唯一真值
命题联结词
有五种联结词,分别为否定、合取、析取、蕴涵、等价。
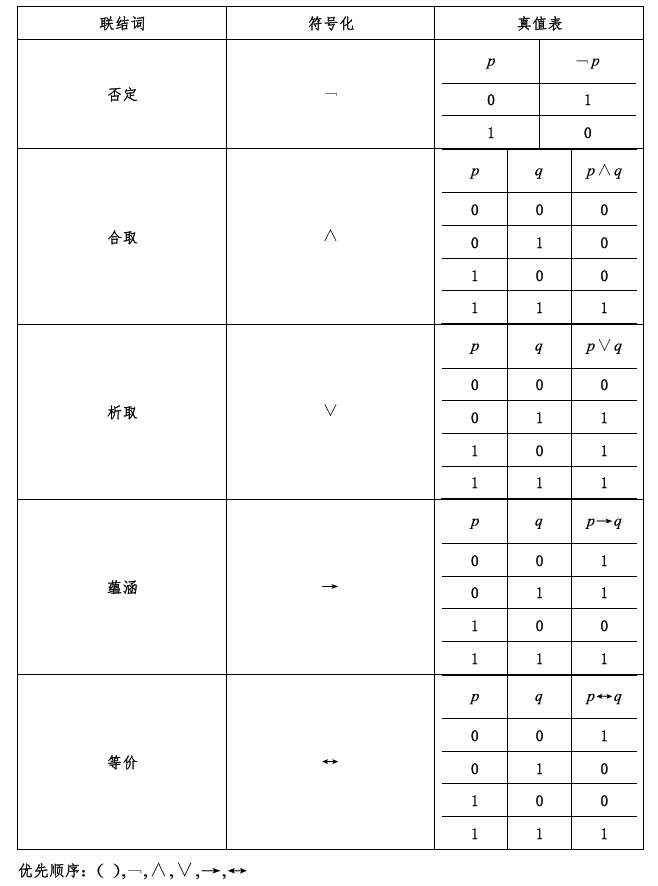
否定:否定的真值与原真值结果相反(相当于数字逻辑中的 “非”)
合取:只有当两个真值都为真时,合取才为真(相当于数字逻辑中的 “与”)
析取:只要有一个真值为真,析取的值就为真(相当于数字逻辑中的 “或”)
蕴涵(需要单独记忆):当p为真且q为假时,p→q为假(1→0 0),其他情况都为真。p q的顺序不能颠倒
只要p,就q 因为p,所以q p仅当q 只有q才p 除非q才p 除非q,否则非p
出现以上几种关键词都应该使用蕴涵联结词
等价:只有p、q真值相同时(二者互为充要条件),二者等价为真
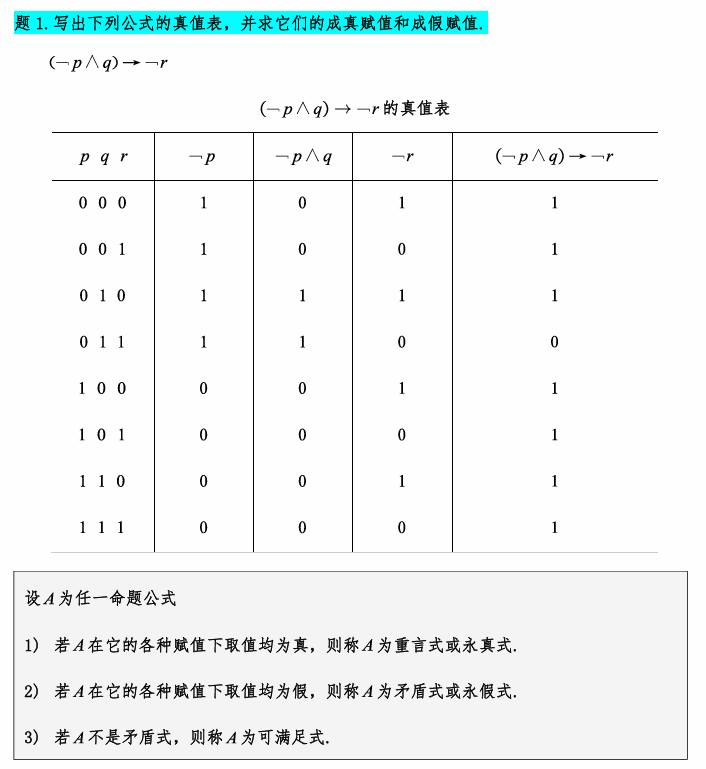
命题公式及其赋值
命题变元:真值可变换的命题
合式公式:将命题变元用联结词或圆括号按一定逻辑关系联结起来的符号串
成真/成假赋值:列出每一个命题变元可能的真值,并给出对应每一组命题真值该合式公式可能的真值
+++
等值式
A,B为两个命题公式,若A,B构成的等价式设A,B是两个命题公式,若A,B构成的等价式A↔B为重言式,则称A与B是等值的,记作A⇔B
常见等值式
双重否定律:A ⟺ ¬¬A
幂等律:A∨A ⟺ A 、A∧A ⟺ A
交换律:A∨B ⟺ B∨A、A∧B ⟺ B∧A
结合律:(A∨B)∨C ⟺ A∨(B∨C)、(A∧B)∧C ⟺ A∧(B∧C)
分配律:A∨(B∧C) ⟺ (A∨B)∧(A∨C)(∨对∧的分配律)
A∧(B∨C) ⟺ (A∧B)∨(A∧C)(∧对∨的分配律)德摩根律:¬(A∨B) ⟺ ¬A∧¬B、¬(A∧B) ⟺ ¬A∨¬B
吸收律:A∨(A∧B) ⟺ A、A∧(A∨B) ⟺ A
零律:A∨1 ⟺ 1、A∧0 ⟺ 0
同一律:A∨0 ⟺ A、A∧1 ⟺ A
排中律:A∨¬A ⟺ 1
矛盾律:A∧¬A ⟺ 0
蕴涵等值式:A→B ⟺ ¬A∨B(
我自己感觉不太好记就加粗了)等价等值式:A↔B ⟺ (A→B)∧(B→A)
——————————以下三个不常考仅作了解——————————
假言易位:A→B ⟺ ¬B→¬A
等价否定等值式:A↔B ⟺ ¬A↔¬B
归谬论:(A→B)∧(A→¬B) ⟺ ¬A
记得找点例题做做巩固一下
析取范式与合取范式
1)文字:命题变元及其否定.
2)简单析取式:仅由有限个文字构成的析取式. p∨q这是一个简单析取式
3)简单合取式:仅由有限个文字构成的合取式. p∧q这是一个简单合取式
4)析取范式:由有限个简单合取式的析取构成的命题式. A1∨A2∨…∨As,其中Ai(i=1,2,3…s)是简单合取式.
5)合取范式:由有限个简单析取式的合取构成的命题式. B1∧B2∧…∧Bt,其中Bi(j=1,2,3…t)是简单析取式.
这个也要自己找例题做
主析取范式与主合取范式
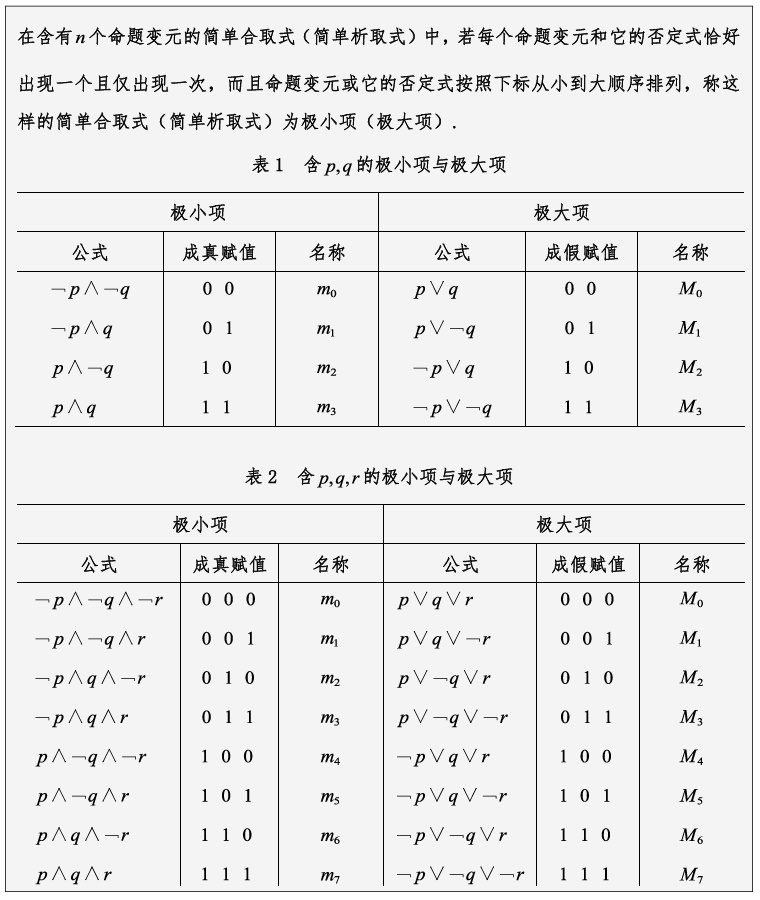
一般用m表示极小项,M表示极大项。右下角的角标为对应的成真赋值/成假赋值看成二进制转成十进制。
-
$$
主析取范式用m_0∨m_1∨m_2∨…∨m_n 表示,
主合取范式M_0∧M_1∧M_2∧…∧M_n 表示
$$
如果某个命题公式有n个命题变元,且已知他的主合取范式为
$$
M_0 ∧ M_3 ∧ … ∧ M_{x-2} ∧ M_x(x=2^n-1)
$$
那么他的主析取范式为
$$
m_1 ∨ m_2 ∨ … ∨m_{x-1}
$$
(极大值和极小值的角标是连贯的从0到x,已知其中的一个主合取范式或析取范式就可以知道另一个式子)要学会用真值表法和直接求两种方法得到主析取范式和主合取范式
例题+2
联结词的完备集
两个新的联结词
↑ :与非联结词( p↑q⇔ ¬(p∧q) )
↓ :或非联结词( p↓q⇔ ¬(p∨q) )
设是一个联结词集合,如果一个命题公式都可以由仅含中的联结词构成的公式表示, 则称是一个联结词完备集.
联结词完备集
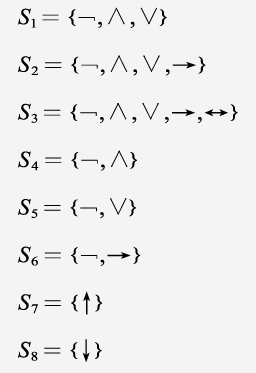
+++
$$
设A和B是两个命题公式,当且仅当A→B是重言式时,称从A可推出B或B是前提A的有效结论,记为A⇒B.
$$
$$
命题公式A_1,A_2,…,A_k推出B的推理正确当且仅当A_1∧A_2∧…∧A_n→B为重言式.
$$
推理的形式结构:
$$
前提:A_1,A_2,…,A_k
$$
$$
结论:B
$$
相关公式
A ⇒ (A ∨ B) 附加律
(A ∧ B) ⇒ A 化简律
(A → B) ∧ A ⇒ B 假言推理
(A → B) ∧ ¬B ⇒ ¬A 拒取式
(A ∨ B) ∧ ¬B ⇒ A 析取三段论
(A → B) ∧ (B → C) ⇒ (A → C) 假言三段论
————————————下面仅做了解,考得不多————————————
(A ↔ B) ∧ (B ↔ C) ⇒ (A ↔ C) 等价三段论
(A → B) ∧ (C → D) ∧ (A ∨ C) ⇒ (B → D) 构造性二难
(A → B) ∧ (¬A → B) ⇒ B 构造性二难特殊形式
(A → B) ∧ (C → D) ∧ (¬B ∨ ¬D) ⇒ (¬A → ¬C) 破坏性二难附加律
自然推理系统
已知前提推导结论。用下面一道例题展示做题流程

思路:根据结论q,在前提中寻找跟q有关的条件,即p ∨ q。要证明则要先得到p,再次寻找跟p有关的前提,即 p → ¬r,以此类推。
做题方法:写证明两个字,每一行中标记序号。先写入已知条件¬t,并标记来源是前提引入。②同理。③是由①②通过拒取式变形得来,需要在后面标记由来(是由哪几个式子通过什么公式变形得到的),以此类推。
把蕴涵式的前键作为附加前提,后键作为结论。最后只要证明蕴涵式右键是个有效结论,那就可以说整个蕴涵式是个有效结论。

一般结论中出现蕴涵式就使用附加前提法
把结论否定作为一个前提,再跟题目中已有前提进行推理,最后得到一个矛盾,就说这个结论是一个有效结论

最后得到结果s与前提¬s矛盾,直接得出¬p是一个有效结论。
如果前提中出现两个以上的结论,需要考虑是否用归谬法
个体词、谓词和量词是谓词逻辑命题符号化的个基本要素.
个体词
个体词:研究对象中可以独立存在的具体的或抽象的客体
个体常项:表示具体或特定的客体的个体词(小智 中国 3)
个体变项:表示抽象或泛指的个体词(如x)
个体域(或称作论域):个体变项的取值范围
全总个体域:由宇宙间一切事物组成的个体域.
谓词
刻画个体词性质及个体词之间相互关系的词.
(4是一个有理数,“是有理数”是一个一元谓词。有几个谓词就称为几元谓词)

谓词逻辑公式及其解释
在公式∀xA和∃xA中,称x为指导变元,A为量词的辖域.在∀x和∃x的辖域中,x的所有出现都称作约束出现,A中不是约束出现的其他变项均称作自由出现.

设A为一公式,若A在任何情况下的任何赋值下均为真,则称A为永真式或逻辑有效式; 若A在任何情况下的任何赋值下均为假,则称A为矛盾式或永假式. 若至少存在一个情况下的一个赋值使A为真,则称A是可满足式.
谓词逻辑等值式与置换规则
设A,B是谓词逻辑中任意两个公式,若A↔B是永真式,则称A与B等值,记作A⇔B, 称A⇔B是等值式.


谓词逻辑前束范式
量词始终在最前面(¬在最前也不算),且只有唯一一组不含量词的公式在最后是前束范式.

(前束范式存在定理)谓词逻辑中的任何公式都存在等值的前束范式.
转换方法
- 把条件或双条件联结词转化;
- 利用量词否定公式,把否定深入到命题变元和谓词公式的前面;
- 换名; (替换公式中的个体变项)
- 利用量词作用域的扩张和收缩等价式,把量词提到前面.
谓词逻辑的推理理论
在谓词逻辑中,从前提A1,A2,…,Ak出发推出结论B的推理的形式结构,依然采用如下的 蕴涵式形式
$$
A_1∧A_2…∧A_k→B
$$
若上式为永真式,则推理正确,否则称推理不正确.


推理和做题过程跟前面命题逻辑推理的方式相同。
集合的基本概念



要分清属于关系(∈)和包含关系(⊂)的区别
属于(∈)是描述元素与集合之间的关系。包含(⊂)是描述集合与集合之间的关系(个人理解
集合的运算

有穷集的计数

“|A|”表示集合A的元素个数
集合恒等式



有序对与笛卡尔积


二元关系


表示关系的三种方法:
- 关系矩阵

R上的二元关系看成坐标(x为行y为列),每个关系对应的坐标标记为1,没有则标记为0
- 关系图

集合A中有四个元素1、2、3、4,在图中用顶点表示。每一个关系代表一条有向边的起点和终点(注意标记箭头)。
- 集合表达式

根据关系图或关系矩阵反推集合表达式
关系的运算



F在左G在右。F中的第二元素跟G中第一元素相同时,保留F的第一元素和G的第二元素,构成一个新的有序对。(右复合)
关系的性质
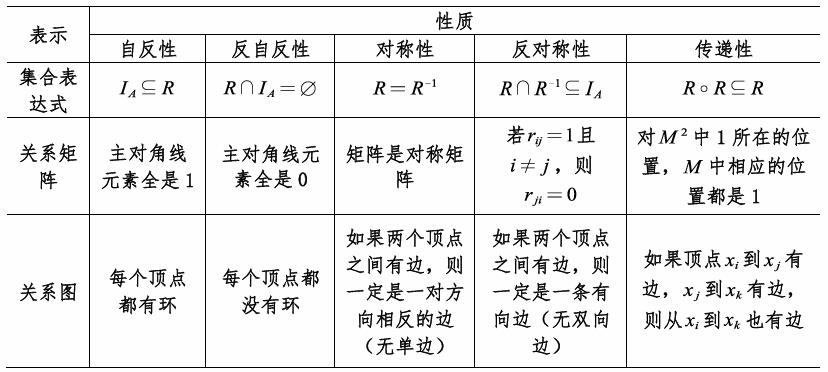
关系的闭包

在关系R上添加对应有序对,使其满足自反(对称或传递),就是对应的自反(对称或传递)闭包。
等价关系与划分



偏序关系

和等价关系区分:等价关系是含有对称性,偏序关系是含有反对称性

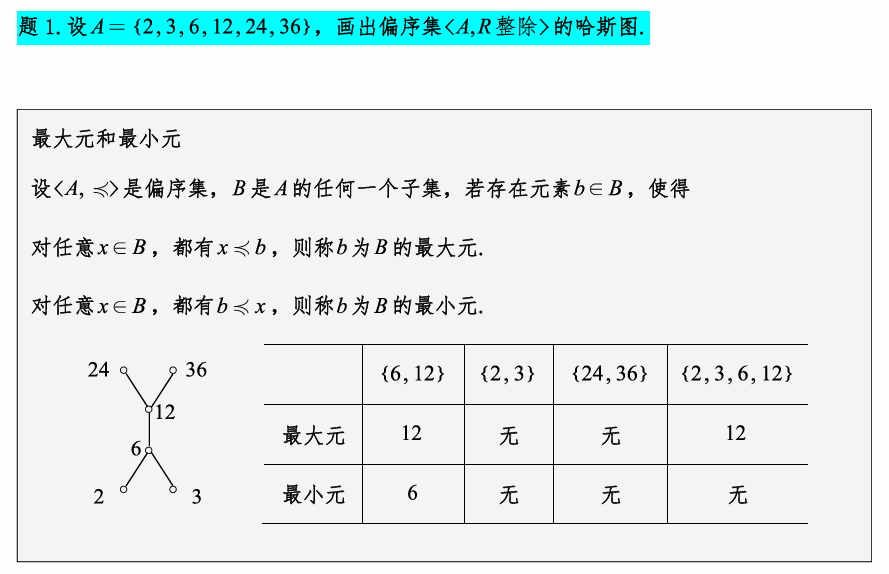
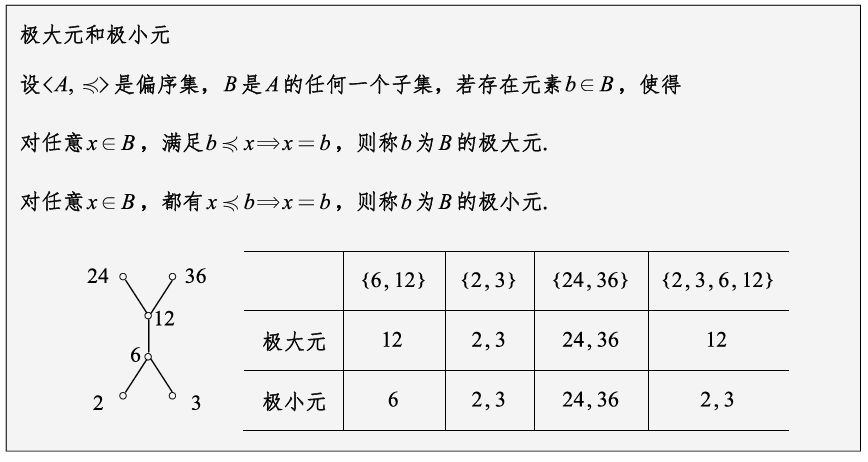
极大、极小元直接看位于哈斯图的上方或下方,在同一高度需要一起列出来,都作为极大、极小值。
从以上定义可以看出,最小元与极小元是不一样的.最小元是B中最小的元素,它与B中其他元素都可比;而极小元不一定与B中元素都可比,只要没有比它小的元素,它就是极小元。对于有穷集B,极小元一定存在,但最小元不一定存在。最小元如果存在,一定是唯一的,但极小元可能有多个。如果B中只有一个极小元,则它一定是B的最小元。类似地,极大元与最大也有这种区别.
哈斯图中的孤立顶点既是极大元,也是极小元.
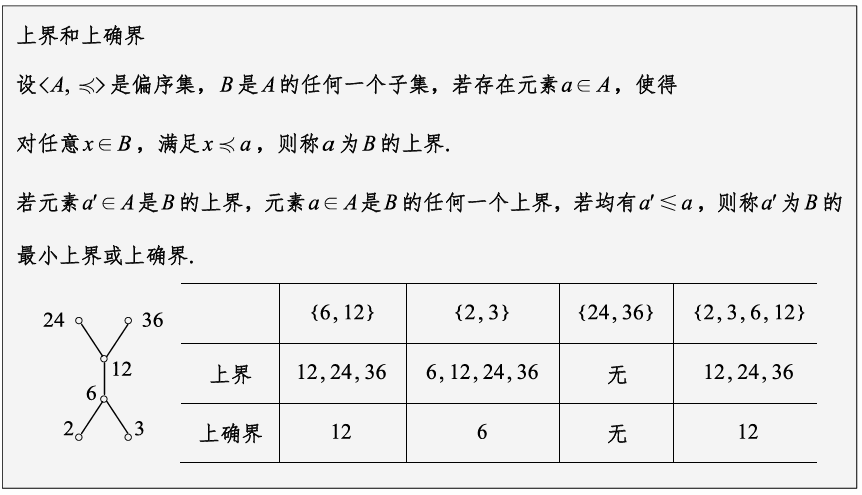
上确界一般是最小上界。上界是大于或等于集合B且能满足偏序条件的集合A中的元素。
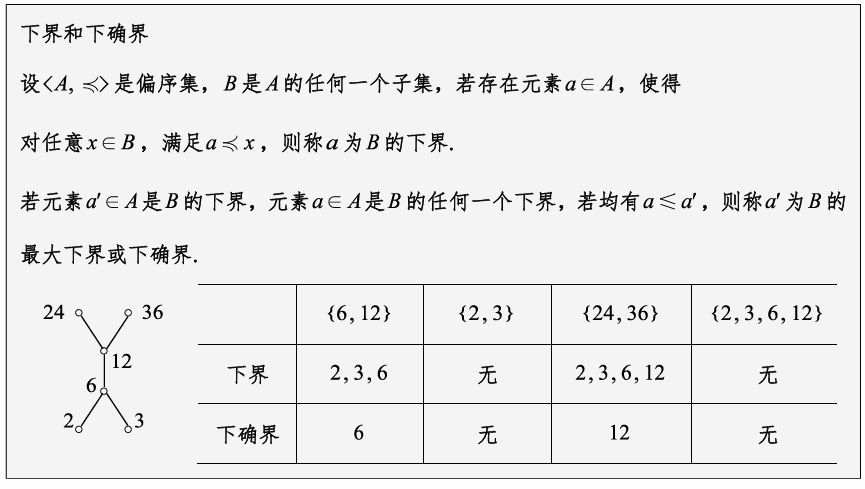
① 子集的上、下界和上、下确界可在集合中寻找;
② 子集的上、下界不一定存在,如果存在可能多个;
③ 子集的上、下确界不一定存在,如果存在一定唯一.
函数的定义和性质

对应F中的每一个x,只有唯一一个y能与之对应。但是能有多个x对应同一个y。
例:

F1中有每一个x都只有一个对应的值,但在F2中的x1能同时对应y1和y2两个值,不唯一,所以F2不是函数

2)函数f的定义域为A,值域为B,就可以记作f: A→B
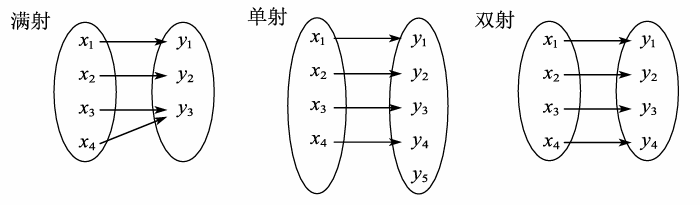
满射:函数的值域中每个元素都有x与之对应
单射:值域中一些元素有x与之对应,有些元素没有x与之对应
双射:同时满足满射和单射。定义域和值域一一对应

函数的复合和反函数



推论1:复合运算满足结合律
推论2:强调f(x)是在括号内(符合运算在左边的函数整体带入右边函数中的x)
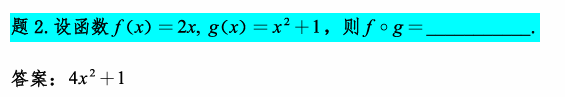
$$
解:原式 = g(f(x))= (2x)^2+1 = 4x^2+1
$$
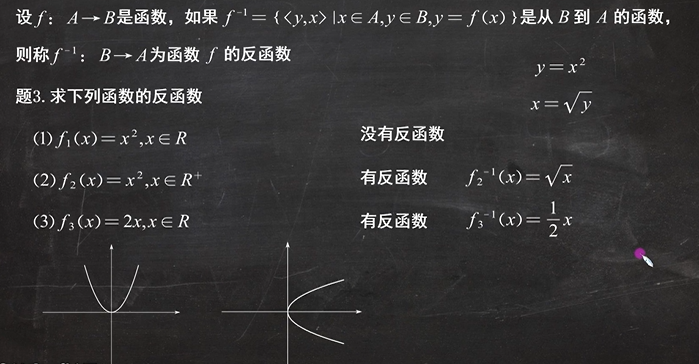
求反函数时可以将图以 y = x 为轴翻转,得到的图像就是该函数的反函数。(tips:若翻转后得到的图像一个x对应2个y值,则该函数没有反函数)
二元运算及其性质

1)判断下面运算是否为集合S上的二元运算
f(<x,y>) = x + y 任意xy都属于自然数集,都可以进行加法运算且结果唯一。对于任意xy,相加之后结果依然是属于自然数集,所以可以说这个运算是自然数集上的二元运算
f(<x,y>) = x + y 满足第一条,但是两个自然数相减后的结果可能为负数,而负数不属于自然数,因此结果不属于S,不满足封闭性

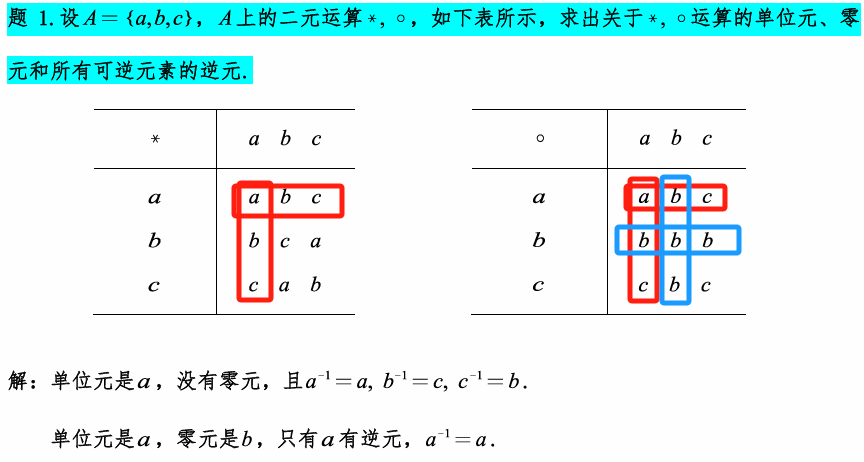
红色方框中表示a*x = x 和 x*a = x,a同时满足左右幺元。蓝色方框中表示 b*x = b 和 x*b = b,b同时满足左右零元。逆元直接看图中哪两个元素
群的定义


图

5/6) 关联:相连的边和顶点之间称为互相关联的。e2和v1的关联次数为1,e1的两个点都是v1,和v1关联次数为2;e1不跟v2相连,关联次数为0
相邻:两个顶点共用一条边称为这两个顶点相邻;两条边有相同的顶点称为两条边相邻


度序列 = 入度序列 + 出度序列

可图画:根据度序列可以构造出一个图
最大度和最小度的符号分别为 Δ(G) 和 δ(G) 。代表图中度数最大和最小的顶点。

通路与回路

图的连通性

无向图顶点存在通路称为x和x连通;有向图顶点存在通路称为x到x可达;
图的矩阵表示
关联矩阵记录顶点和边的关联次数(度数)

$$
m_{ij} =
\begin{cases}
2 & \text{if } v_i = v_j (始点和终点一致)\
1 & \text{if } v_i \neq v_j \
0 & (边与顶点无关联)
\end{cases}
$$
矩阵的行数为顶点个数,列数为边数。

邻接矩阵记录一个顶点到另一个顶点的边数


寻找长度为n的通路就到矩阵的n次方中寻找对应的变数。
$$
如上图求v_2到v_4长度为2的通路条数,需要在矩阵A^2中找到a_{24}(第二行第四列),对应的就是长度为2的条数
$$

欧拉图

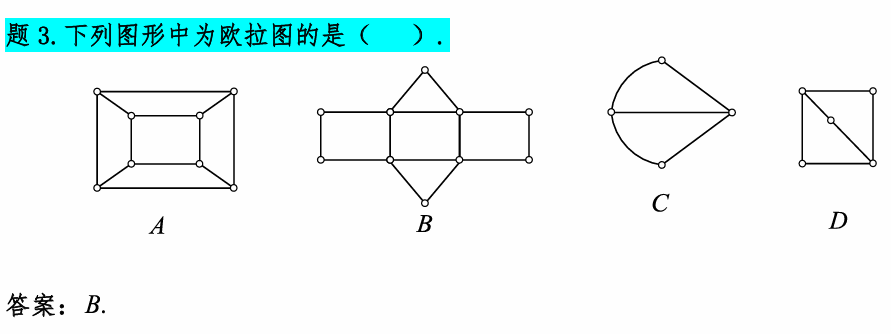
判断无向图直接看顶点度数是否为偶数。B中度数均为2、4,B是欧拉图
哈密顿图

欧拉图是通过所有的边,而哈密顿图是通过所有顶点,两者需要区分开来
最短路问题

最短路径:权相加后最短的路线
一个顶点到自身的路径为0
无向树及其性质

最小生成树

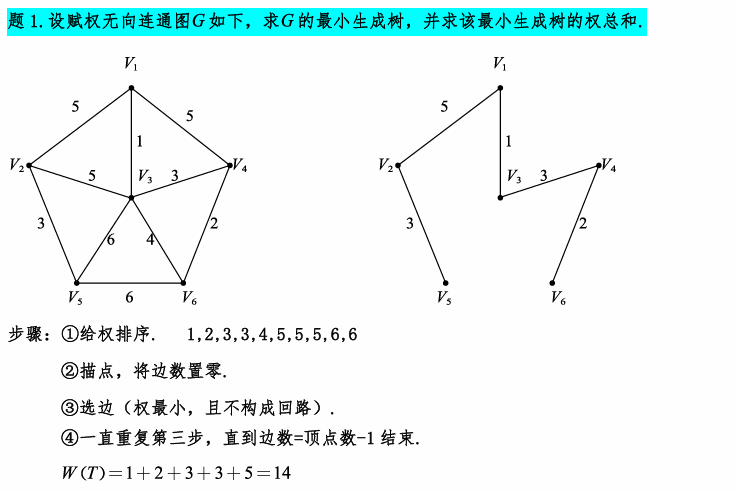
依次列出权1,2,3,3,4,5,5,5,6,6。从权值小的开始描边,描出权值为1、2、3的边,当描权值为4的边时,V3、V4、V6会产生回路,故跳过;描权值为5的边时同理:选择V1-V4一边时,V1、V3、V4会构成回路,所以不选。选V1-V2时,不会产生回路,因此可以选。选完发现已经满足m = n - 1了,最小生成树如上图。
根数及其运用

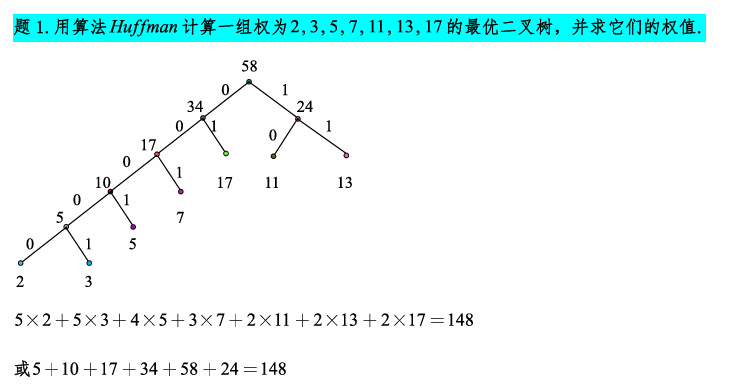
步骤:
①给权排序
②选出两个权最小的顶点,添加新点,权为两点之和
③重复步骤①②,直到只有一个顶点
权值的计算:每个 ( 节点权值*节点的层数 ) 相加

二元前缀码:0-1符号串构成的前缀码
最佳前缀码:由最优二叉树产生的前缀码
如题1图,节点的左边都为0,右边为1,从根出发到权值为2的顶点需要通过00000,那就说这个顶点的最佳前缀码是00000
平面图基本概念


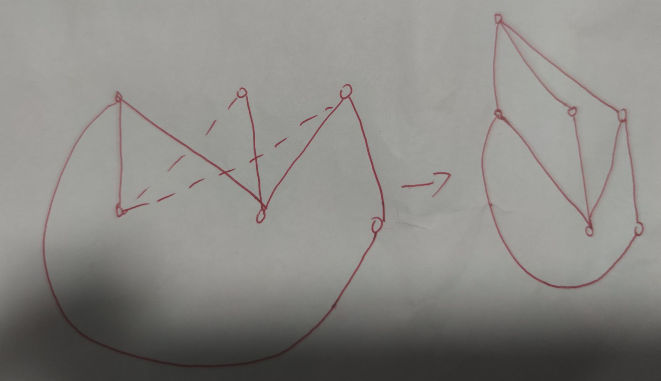
二部图主要是看顶点的相邻关系
以上图为例,顶点可以被分为上面三个和下面三个(分别对应V1和V2),所以可以说这两个图是二部图。同时图1中的第一行第二个顶点只与V2中的第一、二个顶点相连,不是完全二部图;图二中的每一个顶点都与另一边的每个顶点相邻,是完全二部图。
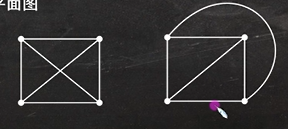
平面图是看除了顶点有无其他相交处
图1中除了顶点,他的几何中心也有一处交点。但是图2中将其中一条相交线绕到矩形之外,除了顶点以外没有其他交点,所以这是一个平面图
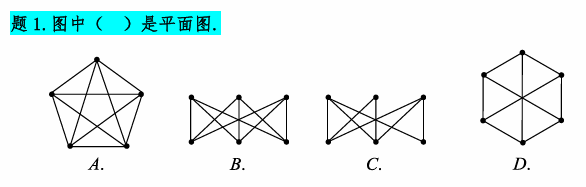
答案为C:
A、B、D除了顶点之外都存在交点,主要疑问在C选项:为什么这么多交点他还是一个平面图,老师给的解释如下
图中将左上角和右下角相邻的线绕到V2下方,左下角的顶点类似翻折一样到V1上方,变形完就不存在交点了所以是平面图(老师还没回我大概是这样理解
欧拉公式



一个简单连通图,若不满足m <= 3n - 6,则一定是非平面图,但满足该不等式的简单连通图未必是平面图.