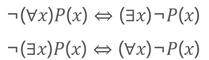1. 绪论

人工智能：用人工方法在机器上实现的智能或使机器具有类似于人的智能

分类：

（1）模拟人的智能：感知智能（视听触觉）、认知智能（语言理解知识推理）、创造智能（灵感顿悟）

（2）不同层次：弱人工智能、通用人工智能、超级人工智能

人工智能涉及多个学科，其研究内容包括知识表示、知识推理、知识应用、机器学习、机器感知、机器思维和机器行为等

  1. 知识表示

知识：人类对自然世界、人类社会、思维方式及运动规律的认识与掌握；是人类在长期的生活及社会实践中、在科学研究及实验中积累起来的经验；是人的大脑通过思维重新组合，把实践中获得的有关信息关联在一起形成的信息结构

在人工智能中将前一种知识称为事实，而把采用“如果……则……”关联起来所形成的知识称为规则 即知识=事实+规则+概念

特性：

（1）相对正确性：在一定条件和环境下，知识一般是正确的。其中”一定的条件和环境“是保证知识正确性必不可少的前提

（2）不确定性：在真和假之间还存在其他中间状态

  • 随机性引起的不确定性
  • 模糊性引起的不确定性
  • 不完全性引起的不确定性
  • 经验依赖引起的不确定性

（3）可表示性：知识可以用适当的形式表示出来（语言、文字、图像、符号、神经网络等）

（4）可利用性：知识的可利用性是指知识可被利用

知识表示：将人类知识形式化或模型化。知识表示过程就是把知识编码成某种数据结构

知识表示=数据结构+处理机制

一阶谓词逻辑表示法

涉及的逻辑分为经典命题逻辑和一阶谓词逻辑，统称为经典逻辑

命题逻辑

命题是一个非真即假的陈述句。判断是否为命题：①陈述句 ②有唯一真值

谓词逻辑

谓词逻辑是基于命题中谓词分析的一种逻辑。一阶谓词逻辑是最直观的一种。

谓词就是用于刻画个体的性质、状态和个体之间关系的语言成分。

一般形式：P(x1,x2,…,xn) P为谓词名，x1、x2为个体

谓词中包含的个体数目称为谓词的元数。有几个个体就是几元谓词

谓词公式

也称为合式公式，是由谓词符号、常量符号、变元符号、函数符号，以及连接词、量词、括号、逗号等按照一定语法规则组成的字符串表达式。

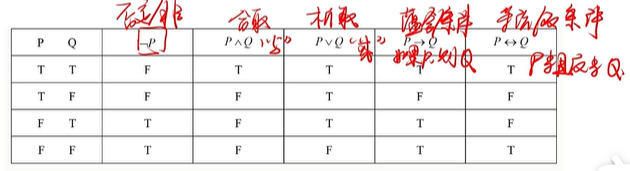
连接词

image-20251219141008644

量词

（1）全称量词：∀A——对个体域中所有个体x/任意一个个体x

​ ”所有学生看书“ (∀A)(student(x) → Have(x,Book))

（2）存在量词：∃x——在个体域中存在个体x

​ ”某个学生在踢球“ (∃x)(student(x) → Plays(x,Football))

位于量词后的单个谓词公式称为量词的辖域。辖域内与量词中同名的变元称为约束变元，不受约束的变元称为自由变元。

image-20251219154307715

性质：谓词公式在不同个体域中具有不同性质

（1）永真性/永假性

谓词公式P对个体域D上任何一个解释都取T/F，则称P在D上永真/假

P在每个非空个体域上永真/假，则P永真/假

（2）可满足性和不可满足性

至少存在一个解释使P在此解释下真值为T，则称公式P可满足，否则P不可满足。

（3）等价性

对共同个体域D上任何解释，P、Q都有相同真值，则称他们在D上等价。

如果D是任意个体域，则称P和Q等价

image-20251219163826975

（4）永真蕴含

对于P、Q，如果P→Q永真，则称公式P永真蕴含Q，记作P ⇒ Q，且称Q为P的逻辑结论，P为Q的前提。

用一阶谓词逻辑表示知识

步骤：

（1）定义谓词、个体

（2）为个体变元赋值

（3）用连接符号连接谓词

状态空间表示法

集合类型：所有可能的状态集合s、操作符集合O、包含问题的初始状态集合s0（是s的非空子集）、目标状态集合

从s0到目标状态集合的路径称为求解路径。求解路径上的操作符序列是状态空间的一个解。

步骤：

（1）定义状态描述形式

（2）用状态描述形式，把问题的所有可能状态都表示出来

（3）定义一组操作符，通过操作符使问题从一种状态转换成另一种状态

（4）绘制状态空间图

image-20251219175450400

产生式的基本形式

确定性事实知识的产生式表示

确定性事实知识一般用三元组表示（对象，属性，值）或（关系，对象1，对象2）

例子 对象 属性 值 结果
雪是白色的 Snow Color White （Snow,Color,White）

不确定性事实知识的产生式表示

比确定性事实多一个置信度（对象，属性，值，置信度）或（关系，对象1，对象2，置信度）置信度为0~1的值

例子 对象 属性 值 置信度 结果
这只狗的名称不太可能叫小白 Dog Name xiaobai 0.2 （Dog，Name，xiaobai，0.2）

确定性规则知识的产生式表示

基本形式：IF P THEN Q 或 P → Q

​ P是产生式的前提（前项），Q是产生式的结论（后项）

​ 例：IF 一个整数大于3 AND 小于5 THEN 是4

不确定性规则知识的产生式表示

同理在最后加一个置信度：IF P THEN Q（置信度） 或 P → Q（置信度）

产生式系统

产生式系统是人工智能系统中常见的一种程序结构，是一种知识表示系统。由规则库、推理机、综合数据库三部分组成。

规则库：初始状态转换成目标状态的各种变化规则

推理机：一个/一组程序组成，负责整个产生式系统运行

综合数据库：存储初始的事实数据、中间结果、最后结果

步骤：

（1）初始化综合数据库，把问题的初始已知事实送入综合数据库

（2）根据相关领域的知识建立规则库

（3）若有未使用的规则，且前提可与综合数据库的事实匹配，跳转（4）；负责跳转（6）.

（4）执行当前规则并做标记，将结论送进综合数据库，若规则结论部分指出的是某些操作则执行

（5）检查综合数据库是否包含问题的解，包含则终止过程；否则跳转（3）

（6）要求用户提供进一步的关于问题的已知事实，提供跳转（3），否则终止

（7）若规则库中不再有未使用的过程，终止

语义网络结构

语义网络由节点和节点间的弧组成。节点表示各种事物、概念、情况、属性、状态、事件和动作等；弧表示它所连接的节点间的各种语义关系。

表示方式：（节点1，弧，节点2）

基本语义关系

  1. 类属关系

指具有共同属性的不同事物之间的分类关系

ISA（Is-A）xx是xx的实例

AMO（A-Member-Of）xx是xx的成员

AKO（A-Kind-Of）xx是xx的类型

image-20251221143404004

（1）鹦鹉是一只鸟 （2）李琦是学生会的成员 （3）鸟是一种动物

  1. 包含关系（聚类关系）

指具有组织或结构特征的部分与整体之间的关系

Part-of——xx是xx的一部分

  1. 属性关系

指事物和属性之间的关系

Have——xx有xx

Can——xx可以xx

  1. 时间关系

事件先后发生关系，节点间不具备属性继承类

Before/After—— xx发生之前/之后xx发生

  1. 位置关系

Located-at（on/under/inside/outside）——xx位于xx

  1. 因果关系

If-then——如果xx则xx

  1. 相近关系

Similar-to——xx像xx

  1. 组成关系

Compose-of——xx由xxxxxx组成

框架表示法

框架是一种描述对象属性的数据结构，是由若干节点和关系构成的网络。

格式：

image-20251221152416606

案例

image-20251221152615276

框架名 <地震3>
地点 下斯洛文尼亚
时间 今天
伤亡数 25
财产损失 5亿美元
震级 8.5
断层 萨迪壕金斯

  1. 确定性推理方法

推理概述

推理：从已知事实出发，按某种策略，运用已掌握知识，推导出其中蕴含的事实性结论或归纳出某些新结论的过程

分类

按推理逻辑分类

演绎推理：从一般到个别（不能增殖新知识）

​ 三段论式：大前提、小前提、结论

归纳推理：从个别到一般（会增殖新知识）

​ ①完全归纳推理：考虑全部对象（如质检每台计算机质量合格）

​ ②不完全归纳推理：只考虑相应事物的部分对象（如随机抽样几台计算机检测质量合格）

默认推理（缺省推理）：完全不知道情况，假设某条件具备进行推理

按所用知识确定性分类

确定性推理：所用知识确定，结论确定，真值只有真或假

不确定性推理：都不确定，真值会位于真假之间

​ ①似然推理（概率论）

​ ②模糊推理（模糊逻辑）

按是否出现反复情况分类

单调推理：随着新知识加入使结论单调增加的趋势

非单调推理：新知识加入否定了前面的结论，回退上一步重新推理

按是否运用启发式知识分类

启发式推理：如解决问题的策略、技巧和经验，以加快推理

非启发式推理：只按照一般控制逻辑进行推理

自然演绎推理

  1. 假言推理

一般形式：P，P→Q ⇒ Q 如果P和P→Q都为真，则可推出Q为真

  1. 拒取式推理·

一般形式：P→Q，¬Q ⇒ ¬P 如果谓词公式P→Q为真且Q为假，则可推出P为假

  1. 三段论式推理

一般形式：P→Q，Q→R ⇒ P→R 如果P→Q，Q→R都为真，则可推出 P→R为真。其中Q称为中项

案例

现有已知事实，小李喜欢所有编程课；所有程序设计语言课都是编程课；Python是一本程序设计语言课。求证：小李喜欢Python

（1）P（x）：x是编程课 L（x，y）：x喜欢y C（x）：x是一门程序设计语言课

（2）P（x）→L（Li，x）、（∀x）[C(x)→P(x)]、C(Python)

（3）P（Python）、P（x）→L（Li，x）→L（Li，Python）

归结演绎推理

⭐谓词公式转换子句集

（1）通过谓词公式的等价性消去谓词公式中的“→”和“↔”

P→Q ⇔ ¬P⋁Q（连接词化归律）

P↔Q ⇔ （¬P⋁Q）⋀（¬Q⋁P）⇔ （P⋀Q）⋁（¬Q⋀¬P）

（2）把否定符号（¬）移到紧靠谓词的位置

¬（P⋀Q）⇔¬P⋁¬Q，¬（P⋁Q）⇔¬P⋀¬Q（德摩根律）

image-20251221192653556

（量词转换率）

（3）变元标准化 把被约束的变元重命名

（4）化为前束形

把所有量词移动到公式前面。但移动不能改变量词的相对位置

（∀x）Q(x)（∃y）R(y) ⇔ （∀x）（∃y）Q(x)R(y)

（5）消去存在量词

①如果存在量词前无全称量词，直接用新个体常量（如abc）替换即可

②若有则用Skolem函数f（x1，x2，…，xn）替换该存在量词约束的变元y

image-20251221193356337

上图中y、z都被约束，分别用f（x）、g（x）代替了

（6）化为Skolem标准形

标准式（∀x1）…（∀xn）M（x1,x2,…，xn）

M（x1,x2,…，xn）由一堆合取的子句构成

P⋁(Q⋀R) ⇔ (P⋁Q)⋀(P⋁R)

P⋀(Q⋁R) ⇔ (P⋀Q)⋁(P⋀R)

（7）消去全称量词

到这里之间去掉就行

（8）消去合取词

消去后把合取词两边内容提取

（9）子句变元标准化

把提取出来的每个合取词统一

  1. 不确定性推理方法

知识不确定性表示

IF E THEN H

CF(H,E)表示该知识的可信度，取值范围为[-1,1]

CF(H,E)>0：证据E增加了结论H的真的程度

CF(H,E)<0：证据E增加了结论H的假的程度

CF(H,E)=1：证据E使结论H为真

CF(H,E)=-1：证据E使结论H为假

CF(H,E)=0：E与H无关

证据不确定性表示

CF(E)，取值范围为[-1,1]

CF(E)>0：证据E以某种程度为真

CF(E)<0：证据E以某种程度为假

CF(E)=1：证据E为真

CF(E)=-1：证据E为假

CF(E)=0：对E的真假程度位置

结论可信度

CF(H)=CF(H,E)*MAX[0,CF(E)]

若出现两条知识推出同一结论⭐

image-20251222162557293

若有三条知识推导出来的结论，先按上图方法求出CF₁₂(H)再与CF₃(H)进行计算

信任函数
$$

Bel(A)=∑_{B⊆D}M(B)
$$
Bel是信任函数、M是概率分布函数

image-20251222182834338

案例

image-20251222182929941

似然函数

image-20251222183057311

案例

image-20251222183256644

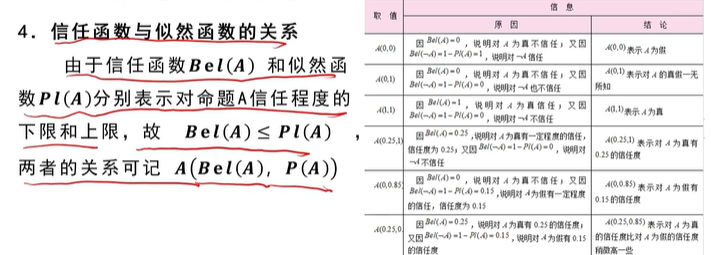
image-20251222184046432

概率分配函数的正交和

image-20251222184357487

案例

image-20251222184832556

类概率函数

image-20251222185552251

案例

image-20251222190718468

image-20251222191022005

image-20251222191052525

不确定性推理步骤

（1）建立样本空间D，确定概率分配函数

（2）假设（证据、知识）的不确定性表示：由经验给出或由规则和事实的信度度量计算基本概率数

（3）组合证据不确定性的算法

（4）不确定性传递算法：计算所有关心的子集A信任函数值Bel（A）、似然函数值Pl（A）

（5）最终由Bel（A）、Pl（A）得出结果

案例

image-20251222192111920

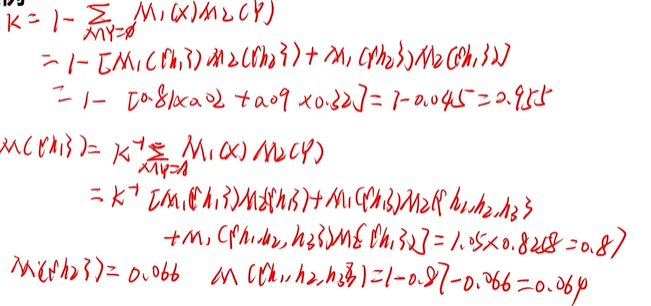
image-20251222192447647

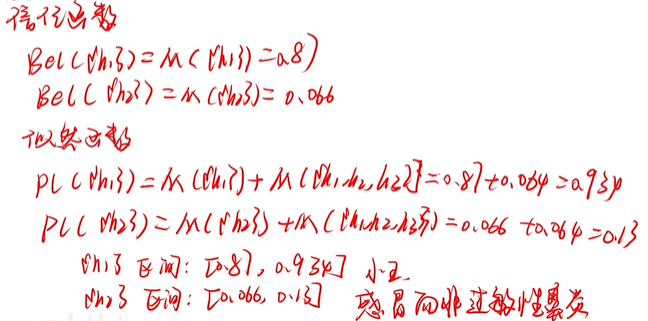
image-20251222192646551

  1. 搜索求解策略

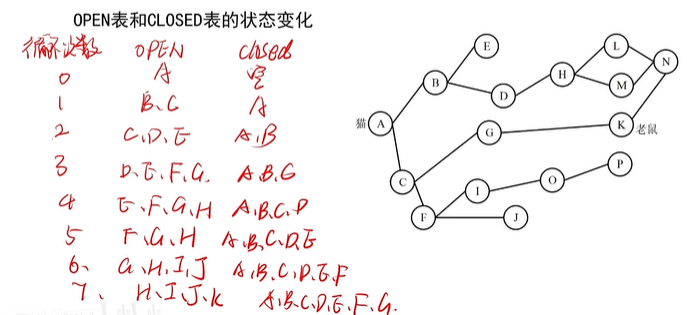
宽度优先搜索

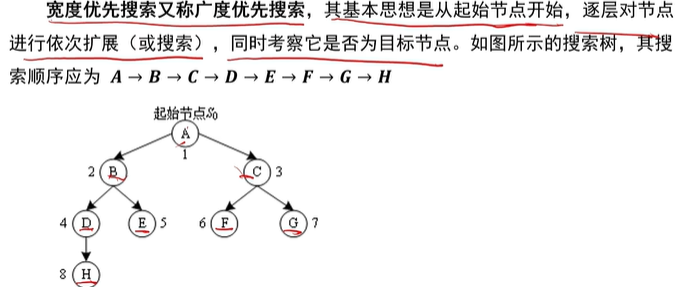
image-20251223091306685

案例

image-20251223091840381

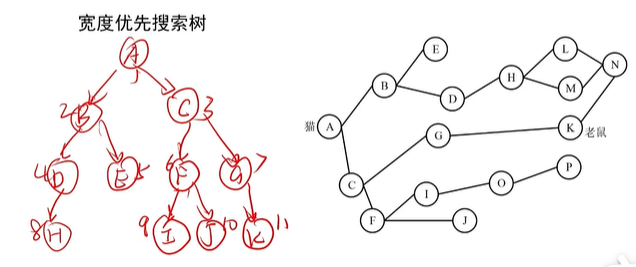
image-20251223091910551

深度优先搜索

估价函数⭐

f(n)=g(n)+h(n) g(n)为初始节点S0到中间节点n（当前位置）的实际代价；h(n)为中间节点n（当前位置）到目标节点G的最优路径估计代价

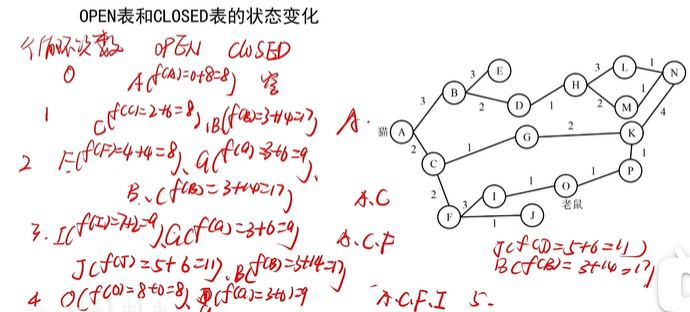
全局择优搜索

对每一个节点选择估价函数值最小的节点作为下一个考察点

案例

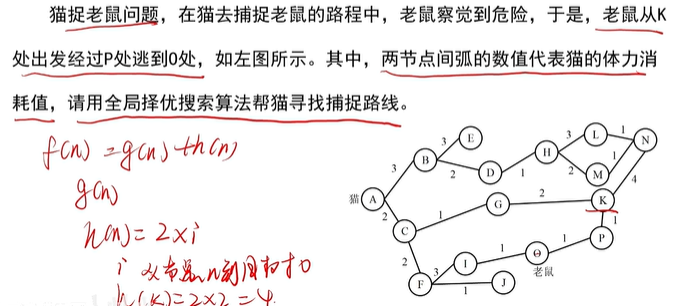
image-20251223094106767

h(n)的值为 2*(当前节点到目标节点数)

image-20251223094629144

局部择优搜索

扩展某一节点后选择估计函数小的节点作为下一考察点

案例

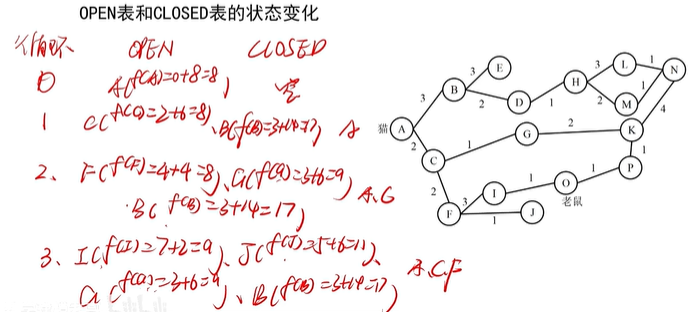
image-20251223095454620

A*搜索

f(n)=g(n)+h(n) 且 h(n)<=h*(n)（从N到目标节点的最小路径）